如图所示,在绕竖直轴匀速转动的水平圆盘盘面上,离轴心r = 20cm处放置一小物块A,其质量m = 2kg,试求:
(1)当圆盘转动的角速度ω = 2rad/s,转动一圈需要的时间是多少?物块A的速度是多少?
(2)A与盘面间的静摩擦力的最大值为其重力的0.5倍,若使A与盘面间不发生相对滑动,则圆盘转动的最大角速度是多大? (取g = 10m/s2)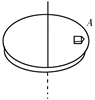
相关知识点
如图所示,在绕竖直轴匀速转动的水平圆盘盘面上,离轴心r = 20cm处放置一小物块A,其质量m = 2kg,试求:
(1)当圆盘转动的角速度ω = 2rad/s,转动一圈需要的时间是多少?物块A的速度是多少?
(2)A与盘面间的静摩擦力的最大值为其重力的0.5倍,若使A与盘面间不发生相对滑动,则圆盘转动的最大角速度是多大? (取g = 10m/s2)