如图所示,一高度为h= 粗糙的水平面在B处与倾角为
粗糙的水平面在B处与倾角为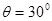 光滑的斜面BC连接,一滑块(可看作质点)从水平面的A点以
光滑的斜面BC连接,一滑块(可看作质点)从水平面的A点以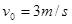 的速度在粗糙的水平面上向右运动,运动到B点时滑块恰能沿光滑斜面下滑。已知AB间的距离
的速度在粗糙的水平面上向右运动,运动到B点时滑块恰能沿光滑斜面下滑。已知AB间的距离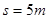 ,取
,取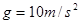 。求:
。求: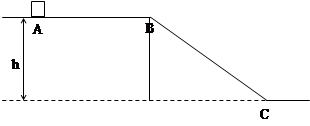
(1)滑块与水平面的动摩擦因数;
(2)若滑块从水平面上的A点以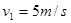 的速度在粗糙的水平面上向右运动,运动到B点后滑块将做什么运动?并求出滑块的着地点与C点的距离。
的速度在粗糙的水平面上向右运动,运动到B点后滑块将做什么运动?并求出滑块的着地点与C点的距离。
如图所示,一高度为h= 粗糙的水平面在B处与倾角为
粗糙的水平面在B处与倾角为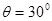 光滑的斜面BC连接,一滑块(可看作质点)从水平面的A点以
光滑的斜面BC连接,一滑块(可看作质点)从水平面的A点以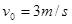 的速度在粗糙的水平面上向右运动,运动到B点时滑块恰能沿光滑斜面下滑。已知AB间的距离
的速度在粗糙的水平面上向右运动,运动到B点时滑块恰能沿光滑斜面下滑。已知AB间的距离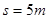 ,取
,取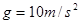 。求:
。求: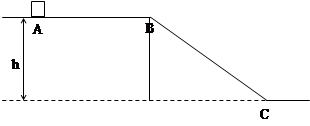
(1)滑块与水平面的动摩擦因数;
(2)若滑块从水平面上的A点以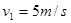 的速度在粗糙的水平面上向右运动,运动到B点后滑块将做什么运动?并求出滑块的着地点与C点的距离。
的速度在粗糙的水平面上向右运动,运动到B点后滑块将做什么运动?并求出滑块的着地点与C点的距离。