(6分)有同学利用如图所示的装置来验证力的平行四边形定则:在竖直木板上铺有白纸,固定两个光滑的滑轮A和B,将绳子打一个结点O,每个钩码的质量相等,当系统达到平衡-时,根据钩码个数读出三根绳子的拉力TOA、TOB和TOC,回答下列问题:
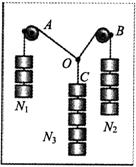
(1)改变钩码个数,实验能完成的是___________
| A.钩码的个数N1=N2=2,N3=4 |
| B.钩码的个数N1=N3=3,N2=4 |
| C.钩码的个数N1=N2=N3=4 |
| D.钩码的个数N1=3,N2=4,N3=5 |
(2)在拆下钩码和绳子前,应该做好三个方面的记录:
_______________________________________________________;
_______________________________________________________;
_______________________________________________________。