在“研究平抛物体的运动”实验中，某同学记录了A、B、 C三点，该同学取A点为坐标原点，建立了右图所示的坐标系。平抛运动轨迹上的这三点坐标值图中已标出。那么A、B两点的时间间隔是________s，小球做平抛运动的初速度大小为___________m/s。（g=10m/s2）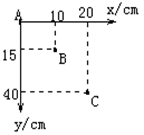
在“研究平抛物体的运动”实验中，某同学记录了A、B、 C三点，该同学取A点为坐标原点，建立了右图所示的坐标系。平抛运动轨迹上的这三点坐标值图中已标出。那么A、B两点的时间间隔是________s，小球做平抛运动的初速度大小为___________m/s。（g=10m/s2）
粤公网安备 44130202000953号