如图所示,质量m=2.0× kg的汽车以不变的速度先后驶过凹形桥面和凸形桥面,两桥面的圆弧半径均为20m。由于轮胎太旧,如果受到超过3×
kg的汽车以不变的速度先后驶过凹形桥面和凸形桥面,两桥面的圆弧半径均为20m。由于轮胎太旧,如果受到超过3× N的压力时就会出现爆胎,则:
N的压力时就会出现爆胎,则: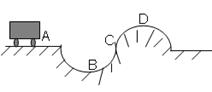
(1)汽车在行驶过程中,在哪个位置最可能出现爆胎?
(2)为了使汽车安全过桥,汽车允许的最大速度是多少?
(3)若以(2)中所求得速度行驶,汽车对桥面的最小压力是多少?
如图所示,质量m=2.0× kg的汽车以不变的速度先后驶过凹形桥面和凸形桥面,两桥面的圆弧半径均为20m。由于轮胎太旧,如果受到超过3×
kg的汽车以不变的速度先后驶过凹形桥面和凸形桥面,两桥面的圆弧半径均为20m。由于轮胎太旧,如果受到超过3× N的压力时就会出现爆胎,则:
N的压力时就会出现爆胎,则:
(1)汽车在行驶过程中,在哪个位置最可能出现爆胎?
(2)为了使汽车安全过桥,汽车允许的最大速度是多少?
(3)若以(2)中所求得速度行驶,汽车对桥面的最小压力是多少?