如图所示,在半径为R的圆形边界内存在竖直向上的匀强电场,电场强度E=1×106T。以圆心为坐标原点建立直角坐标系,在坐标原点分别以竖直向上、竖直向下,水平向左、水平向右同时抛出四个带正电的小球,小球的电荷量q=8×10-12C,质量m=1×10-6kg,它们的初速度大小均为v0=4m/s,忽略空气阻力,重力加速度g="10m/" s2。则:
(1)当R=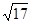 m时,水平向右抛出的小球经过多少时间到达圆形边界?
m时,水平向右抛出的小球经过多少时间到达圆形边界?
(2)试证明,在四个小球都未到达圆形边界前,能用一个圆将四个小球连起来。并写出圆心的坐标。
 角,此后,电子做匀速直线运动,进人磁场并从圆形有界磁场边界上Q点(
角,此后,电子做匀速直线运动,进人磁场并从圆形有界磁场边界上Q点( ,-l)射出,速度沿x轴负方向。不计电子重力。求:
,-l)射出,速度沿x轴负方向。不计电子重力。求:
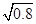 m/s时,物体恰好滑到四分之一圆弧D处。已知A、B的距离L=3.0m,小物块与水平面间的动摩擦因数μ=0.2,半圆形轨道半径R=0.08m。
m/s时,物体恰好滑到四分之一圆弧D处。已知A、B的距离L=3.0m,小物块与水平面间的动摩擦因数μ=0.2,半圆形轨道半径R=0.08m。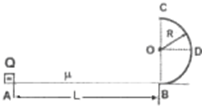
 ,反向电压值为
,反向电压值为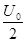 ,且每隔T/2变向1次。现将质量为m的带正电,且电荷量为q的粒子束从AB的中点O以平行于金属板的方向OO′射入,设粒子能全部打在靶上而且所有粒子在A、B间的飞行时间均为T。不计重力的影响,试问:
,且每隔T/2变向1次。现将质量为m的带正电,且电荷量为q的粒子束从AB的中点O以平行于金属板的方向OO′射入,设粒子能全部打在靶上而且所有粒子在A、B间的飞行时间均为T。不计重力的影响,试问: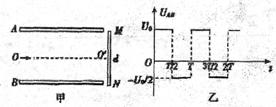
 ,两端各连接A、B小球,质量均为m,杆可以绕距B端1/3处的O轴在竖直平面内自由转动。轻杆由水平位置从静止开始转到竖直方向,求:
,两端各连接A、B小球,质量均为m,杆可以绕距B端1/3处的O轴在竖直平面内自由转动。轻杆由水平位置从静止开始转到竖直方向,求: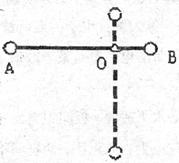
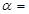 37°,求某时刻质量
37°,求某时刻质量 的小滑块无初速放到斜面上,同时斜面体受到水平向右的推力F作用,滑块恰好相对斜面静止,一起运动2.4m后斜面体下端A碰到障碍物,斜面体速度立即变为零,已知滑块刚放上斜面体时距地高度
的小滑块无初速放到斜面上,同时斜面体受到水平向右的推力F作用,滑块恰好相对斜面静止,一起运动2.4m后斜面体下端A碰到障碍物,斜面体速度立即变为零,已知滑块刚放上斜面体时距地高度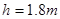 ,斜面体质量
,斜面体质量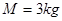 。(
。(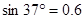 、
、 、取
、取 )求:
)求: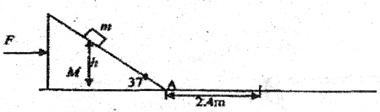
 粤公网安备 44130202000953号
粤公网安备 44130202000953号