如图所示,摆锤。质量为M=2kg,摆杆长为L=0.5m,摆杆质量不计。摆杆初始位置与水平面成α=37°,由静止释放后摆锤绕O轴在竖直平面内做圆周运动,在最低点与质量为m=1kg的铁块(可视为质点)相碰,碰后又上升到图中虚线位置。若铁块与水平面问的动摩擦因数为μ=0.2,求碰后铁块能滑行的距离。(不计空气阻力及转轴处的摩擦,g取10m/s2,sin37°=0.6,cos37°=0.8)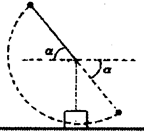
如图所示,摆锤。质量为M=2kg,摆杆长为L=0.5m,摆杆质量不计。摆杆初始位置与水平面成α=37°,由静止释放后摆锤绕O轴在竖直平面内做圆周运动,在最低点与质量为m=1kg的铁块(可视为质点)相碰,碰后又上升到图中虚线位置。若铁块与水平面问的动摩擦因数为μ=0.2,求碰后铁块能滑行的距离。(不计空气阻力及转轴处的摩擦,g取10m/s2,sin37°=0.6,cos37°=0.8)