一小球在桌面上从静止开始做加速运动,现用高速摄影机在同一底片多次曝光,记录下小球每次曝光的位置,并将小球的位置编号。如图所示,1位置恰为小球刚开始运动的瞬间,作为零时刻。摄影机连续两次曝光的时间间隔均为0.5s,小球从1位置到6位置的运动过程中经过各位置的速度分别为:v1=0, v2=0.06 m/s, v3= m/s, v4=0.18 m/s,v5= m/s。在坐标图中作出小球的v-t 图象;并根据v-t 图象求出小球运动的加速度a= m/s2。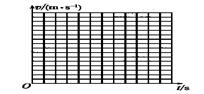
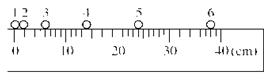
一小球在桌面上从静止开始做加速运动,现用高速摄影机在同一底片多次曝光,记录下小球每次曝光的位置,并将小球的位置编号。如图所示,1位置恰为小球刚开始运动的瞬间,作为零时刻。摄影机连续两次曝光的时间间隔均为0.5s,小球从1位置到6位置的运动过程中经过各位置的速度分别为:v1=0, v2=0.06 m/s, v3= m/s, v4=0.18 m/s,v5= m/s。在坐标图中作出小球的v-t 图象;并根据v-t 图象求出小球运动的加速度a= m/s2。
