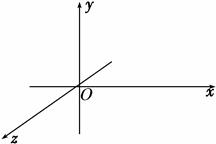
如图所示,Ox、Oy、Oz为相互垂直的坐标轴,Oy轴为竖直方向,整个空间存在竖直向下的匀强磁场,磁感应强度大小为B.现有一质量为m、电量为q的小球从坐标原点O以速度v0沿Ox轴正方向抛出(不计空气阻力,重力加速度为g).求:
(1)若在整个空间加一匀强电场E1,使小球在xOz平面内做匀速圆周运动,求场强E1;
(2)若在整个空间加一匀强电场E2,使小球沿Ox轴做匀速直线运动,求E2的大小;
(3)若在整个空间加一沿y轴正方向的匀强电场E3,使E3=3E1,求该小球从坐标原点O抛出后,经过y轴时的坐标y的表达式.