如图甲所示, A、B、C、D为固定于竖直平面内的闭合绝缘轨道,AB段、CD段均为半径R=1.6m的半圆,BC、AD段水平,AD=BC=8m。B、C之间的区域存在水平向右的有界匀强电场,场强E=5×105V/m,其余区域没有电场。质量为m=4×10-3kg、带电量q=+1×10-8C的小环套在轨道上。小环与轨道AD段的动摩擦因数为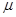 =0.125,与轨道其余部分的摩擦忽略不计。现使小环在D点获得沿轨道向左的初速度v0=4m/s,且在沿轨道DA段运动过程中始终受到方向竖直向上、大小随速度变化的力F(变化关系如图乙所示)作用,小环第一次进入半圆轨道AB时在A点对半圆轨道刚好无压力。不计小环大小,g取10m/s2。求:
=0.125,与轨道其余部分的摩擦忽略不计。现使小环在D点获得沿轨道向左的初速度v0=4m/s,且在沿轨道DA段运动过程中始终受到方向竖直向上、大小随速度变化的力F(变化关系如图乙所示)作用,小环第一次进入半圆轨道AB时在A点对半圆轨道刚好无压力。不计小环大小,g取10m/s2。求:
(1)小环第一次运动到A时的速度大小;
(2)小环第一次回到D点时速度大小;
(3)若小环经过多次循环运动能达到稳定运动状态,则到达D点时的速度至少多大?
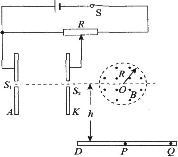
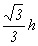 (如图所示),求此时A、K两极板间的电压.
(如图所示),求此时A、K两极板间的电压.

 粤公网安备 44130202000953号
粤公网安备 44130202000953号