【原题】(18分)低空跳伞是一种极限运动,一般在高楼、悬崖、高塔等固定物上起跳。人在空中降落过程中所受空气阻力随下落速度的增大而增大,而且速度越大空气阻力增大得越快。因低空跳伞下落的高度有限,导致在空中调整姿态、打开伞包的时间较短,所以其危险性比高空跳伞还要高。一名质量为70kg的跳伞运动员背有质量为10kg的伞包从某高层建筑顶层跳下,且一直沿竖直方向下落,其整个运动过程的v-t图象如图所示。已知2 0s末的速度为18m/s,10s末拉开绳索开启降落伞,16 2s时安全落地,并稳稳地站立在地面上。g取10m/s2,请根据此图象估算:

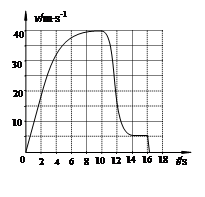
(1)起跳后2s内运动员(包括其随身携带的全部装备)所受平均阻力的大小;
(2)运动员从脚触地到最后速度减为零的过程中,若不计伞的质量及此过程中的空气阻力,则运动员所需承受地面的平均冲击力多大;
(3)开伞前空气阻力对跳伞运动员(包括其随身携带的全部装备)所做的功(结果保留三位有效数字)。