银河系中的某双星由质量不等的星体S1和S2构成,两星在相互之间的万有引力作用下绕两者连线上某一定点C做匀速圆周运动.由天文观察测得其运动周期为T,S1到C点的距离为r1,S2到C点的距离为r2,S1与S2间距为r,已知引力常量为G.则星体S1与S2的质量之和为
A.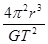 |
B.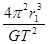 |
C. |
D.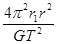 |
银河系中的某双星由质量不等的星体S1和S2构成,两星在相互之间的万有引力作用下绕两者连线上某一定点C做匀速圆周运动.由天文观察测得其运动周期为T,S1到C点的距离为r1,S2到C点的距离为r2,S1与S2间距为r,已知引力常量为G.则星体S1与S2的质量之和为
A.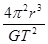 |
B.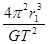 |
C. |
D.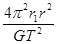 |