倾角θ=370的斜面体固定在水平地面上,一根轻绳跨过固定在斜面顶端的定滑轮,绳的一端与质量为ml="1" kg的物块A连接,且绳与斜面平行;另一端与质量为m2=3kg的物块B连接.开始时,用手按住A,使B悬于距地面高H=0.6m处,而A静止于斜面底端。如图所示.现释放B,试求此后A在斜面上向上滑行的最大距离? (设斜面足够长,且所有接触面间的摩擦均忽略不计,sin370=0.6,cos370=0.8,g取10m/s2)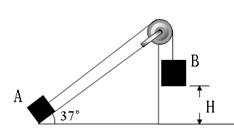
倾角θ=370的斜面体固定在水平地面上,一根轻绳跨过固定在斜面顶端的定滑轮,绳的一端与质量为ml="1" kg的物块A连接,且绳与斜面平行;另一端与质量为m2=3kg的物块B连接.开始时,用手按住A,使B悬于距地面高H=0.6m处,而A静止于斜面底端。如图所示.现释放B,试求此后A在斜面上向上滑行的最大距离? (设斜面足够长,且所有接触面间的摩擦均忽略不计,sin370=0.6,cos370=0.8,g取10m/s2)