在《验证机械能守恒定律》实验中,打的一条纸带如下图所示,O点为打的第一点,选取OP段验证机械能守恒,O,1…P为打的连续的点,打点时间间隔为T,重力加速度为g,下列说法中正确的有( )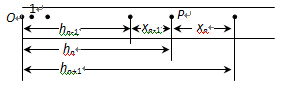
A.打P点时纸带速度用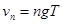 计算 计算 |
B.打P点时纸带速度用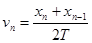 或 或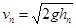 计算 计算 |
| C.O、1两点之间间隔应略小于2mm |
| D.测量重锤质量用天平,不需要测重力 |
E.以h为横坐标,v2为纵坐标,P点(hn,vn2)与坐标原点所连直线斜率的重力加速度g.
在《验证机械能守恒定律》实验中,打的一条纸带如下图所示,O点为打的第一点,选取OP段验证机械能守恒,O,1…P为打的连续的点,打点时间间隔为T,重力加速度为g,下列说法中正确的有( )
A.打P点时纸带速度用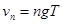 计算 计算 |
B.打P点时纸带速度用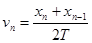 或 或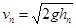 计算 计算 |
| C.O、1两点之间间隔应略小于2mm |
| D.测量重锤质量用天平,不需要测重力 |
E.以h为横坐标,v2为纵坐标,P点(hn,vn2)与坐标原点所连直线斜率的重力加速度g.