小明站在水平地面上,手握不可伸长的细绳一端,细绳的另一端系有质量为m的小球.甩动手腕,使球在竖直平面内绕O以半径L做圆周运动.已知握绳的手离地面的高度为 L,细绳的拉力达到9mg时就会断裂.逐渐增大球的速度,当球某次运动到最低点时绳断裂,忽略手的运动半径和空气阻力,求:
L,细绳的拉力达到9mg时就会断裂.逐渐增大球的速度,当球某次运动到最低点时绳断裂,忽略手的运动半径和空气阻力,求:绳断裂时小球的速度大小v1和小球落地时的速度v2.
小球落地点与O点的水平距离.
控制手离地面的高度不变,减小绳长,使球重复上述运动,若绳仍在球运动到最低点时断裂,要使球飞出的水平距离最大,绳长应为多少?最大水平距离是多少?

 =37°斜向上的力F拉木箱,使木箱沿水平地面匀速运动。已知F=25N,sin37°=0.6,cos37°=0.8。
=37°斜向上的力F拉木箱,使木箱沿水平地面匀速运动。已知F=25N,sin37°=0.6,cos37°=0.8。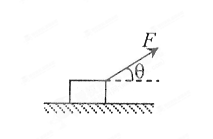
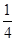 圆周轨道,半径OA处于水平位置,CDO是直径为15m的半圆轨道,两个轨道如图连接固定。一个小球P从A点的正上方距水平半径OA高H处自由落下,沿竖直平面内的轨道运动。通过CDO轨道的最低点C时对轨道的压力力等于其重力的
圆周轨道,半径OA处于水平位置,CDO是直径为15m的半圆轨道,两个轨道如图连接固定。一个小球P从A点的正上方距水平半径OA高H处自由落下,沿竖直平面内的轨道运动。通过CDO轨道的最低点C时对轨道的压力力等于其重力的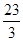 倍.取g为10m/s2.
倍.取g为10m/s2.



 =1060,空气阻力和甲板阻力保持不变,求此时阻拦索承受的张力大小。
=1060,空气阻力和甲板阻力保持不变,求此时阻拦索承受的张力大小。 粤公网安备 44130202000953号
粤公网安备 44130202000953号