如图所示,水平地面上静止放置着物块B和C,相距l=1.0m。物块A以速度v0=10m/s沿水平方向与B正碰。碰撞后A和B牢固地粘在一起向右运动,并再与C发生正碰,碰后瞬间C的速度v=2.0m/s。已知A和B的质量均为 ,C的质量为A质量的K倍,物块与地面的动摩擦因数μ=0.45。(设碰撞时间很短,
,C的质量为A质量的K倍,物块与地面的动摩擦因数μ=0.45。(设碰撞时间很短,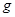 取10m/s2)
取10m/s2)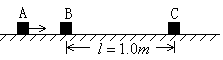
计算与C碰撞前瞬间AB的速度;
根据AB与C的碰撞过程分析K的取值范围,并讨论与C碰撞后AB的可能运动方向。
如图所示,水平地面上静止放置着物块B和C,相距l=1.0m。物块A以速度v0=10m/s沿水平方向与B正碰。碰撞后A和B牢固地粘在一起向右运动,并再与C发生正碰,碰后瞬间C的速度v=2.0m/s。已知A和B的质量均为 ,C的质量为A质量的K倍,物块与地面的动摩擦因数μ=0.45。(设碰撞时间很短,
,C的质量为A质量的K倍,物块与地面的动摩擦因数μ=0.45。(设碰撞时间很短,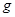 取10m/s2)
取10m/s2)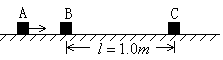
计算与C碰撞前瞬间AB的速度;
根据AB与C的碰撞过程分析K的取值范围,并讨论与C碰撞后AB的可能运动方向。