带电量与质量分别为q,m的离子从离子枪中水平射出,与离子枪相距d处有两平行金属板AB和CD,金属板长和宽也为d,整个空间存在一磁 感强度为B的匀强磁场如图所示。离子垂直于磁场边界中点飞入磁场,不考虑重力的作用,离子的速度应在什么范围内,离子才能打到金属板上?
感强度为B的匀强磁场如图所示。离子垂直于磁场边界中点飞入磁场,不考虑重力的作用,离子的速度应在什么范围内,离子才能打到金属板上?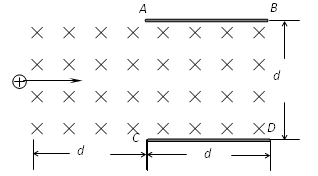
带电量与质量分别为q,m的离子从离子枪中水平射出,与离子枪相距d处有两平行金属板AB和CD,金属板长和宽也为d,整个空间存在一磁 感强度为B的匀强磁场如图所示。离子垂直于磁场边界中点飞入磁场,不考虑重力的作用,离子的速度应在什么范围内,离子才能打到金属板上?
感强度为B的匀强磁场如图所示。离子垂直于磁场边界中点飞入磁场,不考虑重力的作用,离子的速度应在什么范围内,离子才能打到金属板上?