如图所示，将一根长为L的不可伸长的轻质绳子分成等长的两段，绳子的一端悬挂于水平天花板上，另一端共同吊起一个重力为G的物体P并处于静止状态，试求：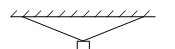
若绳子与天花板的夹角为θ，求绳子张力的大小；
若绳子的最大承受张力为T0=5G/6，要保证绳子不被拉断，求天花板上两悬挂点距离的取值要求。
相关试题
如图10所示，在小车的一端高h的支架上固定着一个半径为R的1/4圆弧光滑导轨，一质量为m =0．2kg的物体从圆弧的顶端无摩擦地滑下，离开圆弧后刚好从车的另一端擦过落到水平地面，车的质量M=2kg，车身长L=0．22m，车与水平地面间摩擦不计，图中h =0．20m，重力加速度g=10m/s2，求R．
设质量为m的子弹以初速度v0射向静止在光滑水平面上的质量为M的木块，并留在木块中不再射出，子弹钻入木块深度为d。（如图9所示）求：
（1）该过程中，木块和子弹组成的系统产生的内能；
（2）木块对子弹的平均阻力的大小；
（3）该过程中木块前进的距离。
发电机输出功率为100kW，输出电压是250V，输电线电阻是15Ω，若输电线中因发热而损失的电功率为输送功率的6%，用户需用220V电压，求：
（1）画出此输电线路的示意图。
（2）在输电线路中设置的升、降压变压器原副线圈的匝数比。
（3）用户得到的电功率是多少？
形轨道安置在同一竖直平面内，两
粤公网安备 44130202000953号