水平地面上有一个半径为R的圆形跑道，高为h的平台边缘上P点在地面上P′点的正上方，P′与跑道圆心O的距离为L（L>R），P′AOC各点均在同一水平直线上，如图所示．已知重力加速度为g，空气阻力不计，小车可视为质点．则：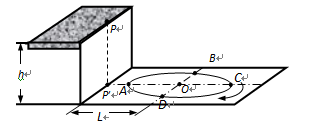
若小车停在跑道上C点时，现从P点水平抛出小沙袋，使其落入小车中，沙袋被抛出时的初速度应为多大？
若小车停在跑道上B点时（∠AOB＝90°），现从P点水平抛出小沙袋，使其落入小车中，沙袋被抛出时的初速度为多大？
相关试题
如图所示，一个半径极小的小球，质量为
，带电量为
，用绝缘丝线悬挂在某水平匀强电场
中，当小球静止时，测得悬线与竖直方向的夹角为
(
，
)，试求：
（1）小球受哪几个力而平衡？
（2）匀强电场的方向；
（3）小球所受电场力的大小及匀强电场E的大小。
如图所示，在倾角为30°的斜面OA左侧有一竖直档板，档板与斜面OA间有垂直纸面向外的匀强磁场，磁感应强度为B=0.2T，档板上有一小孔P，OP=0.6m，现有一质量m=4×10－20kg，带电量q=+2×10－14C的粒子，从小孔以速度v0=3×104m/s水平射进磁场区域．粒子重力不计.
（1）粒子在磁场中做圆周运动的半径是多少？
（2）通过调整粒子进入磁场的速度大小可以控制粒子打到斜面OA时的速度方向，现若要粒子垂直打到斜面OA上，则粒子进入磁场的速度该调整为多少？此情况下粒子打到斜面OA的时间又为多少？
重为G=0.1N的金属棒ab，放在光滑的平行金属导轨上，如图所示，轨道间距为L=0.5m，所在平面与水平面的夹角为30º,匀强磁场垂直于轨道平面向上，电源电动势E=3V，金属棒电阻R=6Ω，其余电阻不计，若金属棒恰好静止，求：
（1）金属棒所受安培力的方向；
（2）磁感应强度的大小。
粤公网安备 44130202000953号