如图所示,两根足够长、电阻不计的光滑平行金属导轨相距为L = 1 m,导轨平面与水平面成θ=30°角,上端连接R=1.5Ω的电阻。质量为m="0.2" kg、阻值r=0.5Ω的金属棒ab放在两导轨上,与导轨垂直并接触良好,距离导轨最上端d =" 4" m,整个装置处于匀强磁场中。磁感应强度B的大小与时间t成正比,磁场的方向垂直导轨平面向上。金属棒ab在沿平行斜面方向的外力F作用下保持静止,当t = 2 s时外力F恰好为零(g =10 m/s2)。求t = 2 s时刻棒的热功率。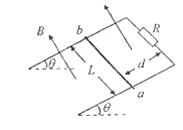
相关知识点
如图所示,两根足够长、电阻不计的光滑平行金属导轨相距为L = 1 m,导轨平面与水平面成θ=30°角,上端连接R=1.5Ω的电阻。质量为m="0.2" kg、阻值r=0.5Ω的金属棒ab放在两导轨上,与导轨垂直并接触良好,距离导轨最上端d =" 4" m,整个装置处于匀强磁场中。磁感应强度B的大小与时间t成正比,磁场的方向垂直导轨平面向上。金属棒ab在沿平行斜面方向的外力F作用下保持静止,当t = 2 s时外力F恰好为零(g =10 m/s2)。求t = 2 s时刻棒的热功率。