如图18(a)所示,一个电阻值为R ,匝数为n的圆形金属线与阻值为2R的电阻R1连结成闭合回路。线圈的半径为r1 . 在线圈中半径为r2的圆形区域存在垂直于线圈平面向里的匀强磁场,磁感应强度B随时间t变化的关系图线如图(b)所示。图线与横、纵轴的截距分别为t0和B0 . 导线的电阻不计。求0至t1时间内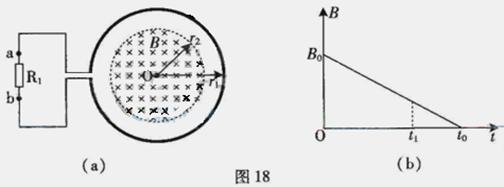
通过电阻R1上的电流大小和方向;
通过电阻R1上的电量q及电阻R1上产生的热量。
相关知识点
如图18(a)所示,一个电阻值为R ,匝数为n的圆形金属线与阻值为2R的电阻R1连结成闭合回路。线圈的半径为r1 . 在线圈中半径为r2的圆形区域存在垂直于线圈平面向里的匀强磁场,磁感应强度B随时间t变化的关系图线如图(b)所示。图线与横、纵轴的截距分别为t0和B0 . 导线的电阻不计。求0至t1时间内
通过电阻R1上的电流大小和方向;
通过电阻R1上的电量q及电阻R1上产生的热量。