如图所示，一个半径R=1.0m的圆弧形光滑轨道固定在竖直平面内，轨道的一个端点B和圆心O的连线与竖直方向夹角θ=60°，C为轨道最低点，D为轨道最高点．一个质量m=0.50kg的小球（视为质点）从空中A点以v0=4.0m/s的速度水平抛出，恰好从轨道的B端沿切线方向进入轨道．重力加速度g取10m/s2．试求：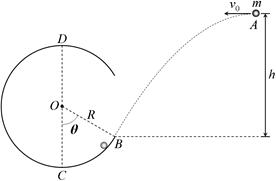
小球抛出点A距圆弧轨道B端的高度h．
小球经过轨道最低点C时对轨道的压力FC．
小球能否到达轨道最高点D？若能到达，试求对D点的压力FD．若不能到达，试说明理由．
皮带装置如图所示，其中AB段是水平的，长度LAB＝4 m，BC段是倾斜的，长度lBC＝5 m，倾角为θ＝37°，AB和BC在B点通过一段极短的圆弧连接（图中未画出圆弧），传送带以v＝4 m/s的恒定速率顺时针运转．已知工件与传送带间的动摩擦因数μ＝0.5，重力加速度g取10 m/s2.现将一个工件（可看做质点）无初速度地放在A点，求：
（1）工件第一次到达B点所用的时间：
（2）工件沿传送带上升的最大高度；
（3）工件运动了23 s时所在的位置．
1935年在苏联的一条直铁轨上，有一列火车因蒸汽不足而停驶，驾驶员把货车厢甲留在现场，只拖着几节车厢向前方不远的车站开进，但他忘了将货车厢刹好，使车厢在斜坡上以4m/s的速度匀速后退，此时另一列火车乙正以16m/s的速度向该货车厢驶来，驾驶技术相当好的驾驶员波尔西列夫立即刹车，紧接着加速倒退，结果恰好接住了货车厢甲，从而避免了相撞．设列车乙刹车过程和加速倒退过程均为匀变速直线运动，且加速度大小均为2m/s2，求波尔西列夫发现货车厢甲向自己驶来而立即开始刹车时，两车相距多远？
如图所示，轻弹簧的两端与质量均为2m的B、C两物块固定连接，静止在光滑水平面上，物块C紧靠挡板但不粘连．另一质量为m的小物块A以速度V0从右向左与B发生弹性正碰，碰撞时间极短可忽略不计．（所有过程都在弹簧弹性限度范围内）求：
（1）A、B碰后瞬间各自的速度；
（2）弹簧第一次压缩最短与第一次伸长最长时弹性势能之比．
A、B为竖直墙壁上等高的两点，AO、BO为长度相等的两根轻绳，CO为一根轻杆。转轴C在AB中点D的正下方，AOB在同一水平面上。∠AOB=90º，∠COD=60º。若在O点处用轻绳悬挂一个质量为m的物体，求平衡后绳AO所受拉力的大小。
粤公网安备 44130202000953号