如图所示，两带电平行板A、B间的电场为匀强电场，场强E=8.0×102V/m，两板间距d=16cm，板长L=30cm。一带电量q=1.0×10-16C、质量m=1.0×10-24kg的粒子以v0=3×105m/s的速度沿平行于板方向从两板的正中间射入电场后向着B板偏转，不计带电粒子的重力，求：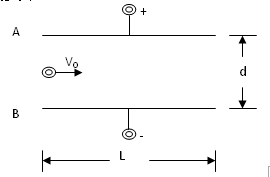
粒子待何种电荷？在电场中运动时间为多久？
粒子废除电场时的偏转角的正弦值为多大
如图所示，一闭合线圈有200匝，总电阻R＝5Ω，穿过它的磁通量在0.2 s内由6×10 -3 Wb增加到1.2×10-2 Wb，求：
（1）线圈中磁通量的变化量
（2）线圈中磁通量的变化率
（3）线圈中产生的感应电动势E大小
一根长L= 30cm的导线垂直磁感线方向放入如图所示的匀强磁场中，通入向右的电流。
（1）当导线中通以I1 = 2A的电流时，导线受到的安培力大小为 1.8×10-6N，则该磁场的磁感应强度为多少？
（2）若该导线中通以
的电流，则此时导线所受安培力大小是多少？方向如何？
已知一带负电的试探电荷电量为-1.0×10-6 C，置于电场中的A点，受到竖直向下的电场力，大小为2.0×10-4N，
（1）电场中A点的电场强度大小和方向；
（2）若将电量为＋1.6×10-8 C的试探电荷放在A点，求它受到的电场力大小和方向。
如图所示，绝缘的水平桌面上方有一竖直方向的矩形区域，该区域是由三个边长均为L的正方形区域ABFE、BCGF和CDHG首尾相接组成的，且矩形的下边EH与桌面相接．三个正方形区域中分别存在方向为竖直向下、竖直向上、竖直向上的匀强电场，其场强大小比例为1∶1∶2．现有一带正电的滑块以某一初速度从E点射入场区，初速度方向水平向右，滑块最终恰从D点射出场区．已知滑块在ABFE区域所受静电力和所受重力大小相等，桌面与滑块之间的动摩擦因数为0.125，重力加速度为g，滑块可以视作质点．
求： （1）滑块进入CDHG区域时的速度大小v0；
（2）滑块在ADHE区域运动的总时间．
粤公网安备 44130202000953号