如下图所示的电路中,电源电动势E=6.00V,其内阻可忽略不计。电阻的阻值分别为R1=2.4kΩ、R2=4.8kΩ,电容器的电容C=4.7μF。闭合开关S,待电流稳定后,用电压表测R1两端电压,其稳定值为1.50V。该电压表的内阻为多大?
由于电压表的接入,电容器的带电量变化了多少?
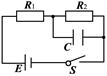
如下图所示的电路中,电源电动势E=6.00V,其内阻可忽略不计。电阻的阻值分别为R1=2.4kΩ、R2=4.8kΩ,电容器的电容C=4.7μF。闭合开关S,待电流稳定后,用电压表测R1两端电压,其稳定值为1.50V。该电压表的内阻为多大?
由于电压表的接入,电容器的带电量变化了多少?
