如右图所示,半径R=0.9m的四分之一圆形光滑轨道竖直放置,圆弧最低点B与长为L=1m的水平面相切于B点,BC离地面高h=0.45m,C点与一倾角为θ= 30°的光滑斜面连接,质量为m=1.0 kg的小滑块从圆弧顶点D由静止释放,已知滑块与水平面间的动摩擦因数µ=0.1,取g=10m/s2.试求:
(1)小滑块刚到达圆弧的B点时对圆弧的压力?
(2)小滑块到达C点时的速度?
(3)通过计算说明小滑块离开C点后是直接落到地面上还是直接落到斜面上?
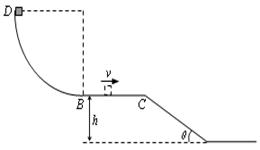
如右图所示,半径R=0.9m的四分之一圆形光滑轨道竖直放置,圆弧最低点B与长为L=1m的水平面相切于B点,BC离地面高h=0.45m,C点与一倾角为θ= 30°的光滑斜面连接,质量为m=1.0 kg的小滑块从圆弧顶点D由静止释放,已知滑块与水平面间的动摩擦因数µ=0.1,取g=10m/s2.试求:
(1)小滑块刚到达圆弧的B点时对圆弧的压力?
(2)小滑块到达C点时的速度?
(3)通过计算说明小滑块离开C点后是直接落到地面上还是直接落到斜面上?
