(本题满分13分)
把一颗骰子投掷两次,记第一次出现的点数为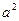 ,第二次出现的点数为
,第二次出现的点数为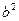 (其中
(其中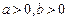 ).
).
(Ⅰ)若记事件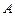 “焦点在
“焦点在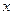 轴上的椭圆的方程为
轴上的椭圆的方程为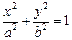 ”,求事件
”,求事件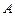 的概率;
的概率;
(Ⅱ)若记事件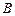 “离心率为2的双曲线的方程为
“离心率为2的双曲线的方程为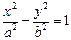 ”,求事件
”,求事件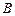 的概率.
的概率.
推荐套卷
(本题满分13分)
把一颗骰子投掷两次,记第一次出现的点数为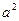 ,第二次出现的点数为
,第二次出现的点数为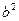 (其中
(其中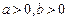 ).
).
(Ⅰ)若记事件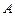 “焦点在
“焦点在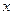 轴上的椭圆的方程为
轴上的椭圆的方程为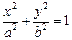 ”,求事件
”,求事件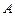 的概率;
的概率;
(Ⅱ)若记事件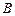 “离心率为2的双曲线的方程为
“离心率为2的双曲线的方程为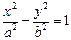 ”,求事件
”,求事件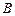 的概率.
的概率.