宇宙中存在由质量相等的四颗星组成的四星系统,四星系统离其他恒星较远,通常可忽略其他星体对四星系统的引力作用.已观测到稳定的四星系统存在两种基本的构成形式:一种是四颗星稳定地分布在边长为a的正方形的四个顶点上,均围绕正方形对角线的交点做匀速圆周运动,其运动周期为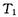 ;另一种形式是有三颗星位于边长为a的等边三角形的三个项点上,并沿外接于等边三角形的圆形轨道运行,其运动周期为
;另一种形式是有三颗星位于边长为a的等边三角形的三个项点上,并沿外接于等边三角形的圆形轨道运行,其运动周期为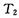 ,而第四颗星刚好位于三角形的中心不动.试求两种形式下,星体运动的周期之比
,而第四颗星刚好位于三角形的中心不动.试求两种形式下,星体运动的周期之比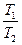 .
.
宇宙中存在由质量相等的四颗星组成的四星系统,四星系统离其他恒星较远,通常可忽略其他星体对四星系统的引力作用.已观测到稳定的四星系统存在两种基本的构成形式:一种是四颗星稳定地分布在边长为a的正方形的四个顶点上,均围绕正方形对角线的交点做匀速圆周运动,其运动周期为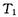 ;另一种形式是有三颗星位于边长为a的等边三角形的三个项点上,并沿外接于等边三角形的圆形轨道运行,其运动周期为
;另一种形式是有三颗星位于边长为a的等边三角形的三个项点上,并沿外接于等边三角形的圆形轨道运行,其运动周期为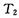 ,而第四颗星刚好位于三角形的中心不动.试求两种形式下,星体运动的周期之比
,而第四颗星刚好位于三角形的中心不动.试求两种形式下,星体运动的周期之比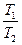 .
.