如图所示,一束电子从x轴上的A点以平行于y轴的方向射入第一象限区域,射入的速度为v0,电子质量为m,电荷量为e.为了使电子束通过y轴上的B点,可在第一象限的某区域加一个沿x轴正方向的匀强电场,此电场的电场强度为E,电场区域沿x轴方向为无限长,沿y轴方向的宽度为s,且已知OA=L,OB=2s,求该电场的下边界与B点的距离。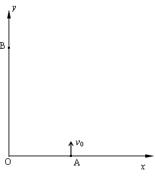
如图所示,一束电子从x轴上的A点以平行于y轴的方向射入第一象限区域,射入的速度为v0,电子质量为m,电荷量为e.为了使电子束通过y轴上的B点,可在第一象限的某区域加一个沿x轴正方向的匀强电场,此电场的电场强度为E,电场区域沿x轴方向为无限长,沿y轴方向的宽度为s,且已知OA=L,OB=2s,求该电场的下边界与B点的距离。