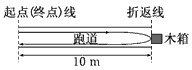
“10米折返跑”的成绩反映了人体的灵敏素质。测定时,在平直跑道上,受试者以站立式起跑姿势站在起点(终点)线前,听到起跑的口令后,全力跑向正前方10米处的折返线,测试员同时开始计时。受试者到达折返线处,用手触摸折返线处的物体(如木箱)后,再转身跑向起点(终点)线,当胸部到达起点(终点)线的垂直面时,测试员停止计时,所用时间即为“10米折返跑”的成绩,如图所示。设受试者起跑的加速度为4 m/s2,运动过程中的最大速度为4 m/s,快到达折返线处时需减速到零,减速的加速度为8 m/s2,返回时达到最大速度后不需减速,保持最大速度冲线.求该受试者“10米折返跑”的成绩为多少?