如图所示，在光滑桌面上放着木板A，长度为L=1.0m，在木板A的左上端放一可视为质点的小金属块，它的质量和木板的质量相等，最初它们是静止的。现让小金属块以V0 =2.0m/s的初速度开始向右滑动，当滑动到木板A的右端时，滑块的速度为V1="1m/s," 取 g= l0m/s2，求：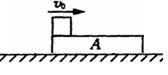
小金属块刚滑过木板A时的速度及滑块与木板间的摩擦因数；
木板Ａ的位移。
相关试题
如图所示，在光滑桌面上放着木板A，长度为L=1.0m，在木板A的左上端放一可视为质点的小金属块，它的质量和木板的质量相等，最初它们是静止的。现让小金属块以V0 =2.0m/s的初速度开始向右滑动，当滑动到木板A的右端时，滑块的速度为V1="1m/s," 取 g= l0m/s2，求：小金属块刚滑过木板A时的速度及滑块与木板间的摩擦因数；
木板Ａ的位移。
分子的平均间距（取两位有效数字）
，体积为
的一小块金刚石中含有多少碳原子？并估算碳原子的直径（取两位有效数字）
的油膜，试估算油分子直径的大小．
，宽
，高
，试在标准状态下估算空气分子间的平均距离，并比较这个距离和分子直径的数量级．
粤公网安备 44130202000953号