某游乐场的过山车从较高的弧形轨道顶部，从静止开始向下运动，在底部进入与之连接的圆形轨道，它可以底朝上在竖直圆轨道顶部运行，游客不会掉下来，如图（甲）所示，可以把这种情形抽象为如图（乙）所示的简图，为了游客的安全，载人过山车在通过圆轨道的最高点时，对轨道要有一定的压力，假设该压力为人与过山车总重力的0.5倍，圆轨道的半径为R，不考虑一切阻力，问：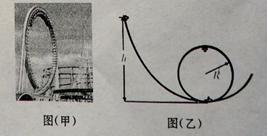
弧形轨道顶部到底部的高度
应多大？若人的质量为
，过山车经过圆轨道最低点时人对座椅的压力多大？
相关试题
如图所示电路，变阻器R1最大阻值为4Ω,此时它的有效阻值为2Ω，定值电阻R2=6Ω，电源内阻r=1Ω，当开关闭合时，电源消耗的总功率为16W，输出功率为12W，此时电灯恰好正常发光，求：
电源的热功率；
电源的电动势；
电灯的电阻。
如图所示，长L、质量为m的金属杆ab，被两根竖直的金属丝静止吊起，金属杆ab处在方向垂直纸面向里的匀强磁场中．当金属杆中通有方向a →b的电流I时，每根金属丝的拉力大小为T．当金属杆通有方向b→a的电流I时，每根金属丝的拉力大小为2T．求磁场的磁感应强度B的大小．
A为已知电场中的一固定点，在A点放一个电荷量为q的点电荷，所受的电场力为F,则A点的场强为E是多少？若在A点放一个电荷量为2q的点电荷,则A点的场强为E是多少？
相关知识点
粤公网安备 44130202000953号