如图所示，分布在半径为r的圆形区域内的匀强磁场，磁感应强度为B，方向垂直纸面向里。电量为q、质量为m的带正电的粒子从磁场边缘A点沿圆的半径AO方向射入磁场，离开磁场时速度方向偏转了60°角（重力忽略不计）。试确定：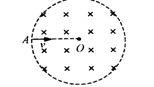 
粒子做圆周运动的半径。
粒子的入射速度
如图所示，滑块的质量M=2kg，开始静止在水平面上的A点，滑块与水平面间的摩擦因数为μ=0.2，与A点相距S=2.25m的B点上方有一质量m=1.2kg的小球，小球被一长为l=0.5米的轻绳挂在O点而处于静止状态。现给滑块一瞬时冲量I=10N・S，让滑块沿水平面向右运动，此后与小球发生碰撞，碰后小球恰能在竖直平面内完成完整的圆周运动（g=10m/s2）。求：
（1）滑块最终静止在距离A点多远处？
（2）因滑块与小球碰撞而损失的机械能是多少？
如图所示，真空中金属板M、N相距为d，当N板用波长为λ的光照射时，电路中的电流恒为I.设电子的电荷量为e，质量为m，真空中光速为c.
（1）求每秒到达M板的电子数.
（2）当垂直于纸面再加一匀强磁场，且磁感应强度为B时，电路中的电流恰好为零，求从N板逸出光电子的最大初动能和N板的逸出功.
如图12所示质量为M的小物块A静止在离地面高h的水平桌面的边缘，质量为m的小物块B沿桌面向A运动并以速度v0与之发生正碰（碰撞时间极短）。碰后A离开桌面，其落点离出发点的水平距离为L。碰后B反向运动。已知B与桌面的动摩擦因数为μ，重力加速度为g，桌面足够长。求
（1）碰后A、B小物块分离的瞬间速率各是多少？
（2）碰后小物块B后退的最大距离是多少？
一人用一根长L=1m，最大只能承受T=46N拉力的轻绳子，拴着一个质量m=1kg的小球（不考虑其大小），在竖直平面内作圆周运动，已知圆心O离地高H=21m，如图7所示，若小球运动到达最低点时绳刚好被球拉断，求
（1）小球到达最低点的速度大小是多少?
（2）小球落地点到O点的水平距离是多少?（g=10m/s2）
粤公网安备 44130202000953号