如图所示,质量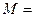 20kg的物体从光滑曲面上高度
20kg的物体从光滑曲面上高度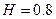 m处释放,到达底端时水平进入水平传送带,传送带由一电动机驱动着匀速向左转动,速率恒为3m/s.已知物体与传送带间的动摩擦因数
m处释放,到达底端时水平进入水平传送带,传送带由一电动机驱动着匀速向左转动,速率恒为3m/s.已知物体与传送带间的动摩擦因数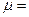 0.1.(g取10m/s2)
0.1.(g取10m/s2)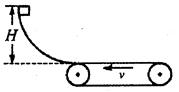
若两皮带轮之间的距离是6m,物体冲上传送带后就移走光滑曲面,物体将从哪一边离开传送带?通过计算说明你的结论.
若皮带轮间的距离足够大,从M滑上到离开传送带的整个过程中,由于M和传送带间的摩擦而产生了多少热量?
如图所示,质量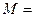 20kg的物体从光滑曲面上高度
20kg的物体从光滑曲面上高度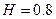 m处释放,到达底端时水平进入水平传送带,传送带由一电动机驱动着匀速向左转动,速率恒为3m/s.已知物体与传送带间的动摩擦因数
m处释放,到达底端时水平进入水平传送带,传送带由一电动机驱动着匀速向左转动,速率恒为3m/s.已知物体与传送带间的动摩擦因数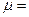 0.1.(g取10m/s2)
0.1.(g取10m/s2)
若两皮带轮之间的距离是6m,物体冲上传送带后就移走光滑曲面,物体将从哪一边离开传送带?通过计算说明你的结论.
若皮带轮间的距离足够大,从M滑上到离开传送带的整个过程中,由于M和传送带间的摩擦而产生了多少热量?