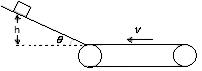
以36Km/h速度行驶的列车开始下坡,在坡路上的加速度是0.2m/s2,经过30s到达坡底,求坡路的长度和到达坡底时的速度?
粤ICP备20024846号
 粤公网安备 44130202000953号
粤公网安备 44130202000953号
 粤公网安备 44130202000953号
粤公网安备 44130202000953号
Copyright ©2020-2024 优题课 youtike.com 版权所有
Powered by:Youtike Platform 6.6.3
声明:本网站部分内容由互联网用户自发贡献自行上传,本网站不拥有所有权,也不承担相关法律责任。
如果您发现有涉嫌版权的内容,欢迎发送邮件至:service@youtike.com 或 联系QQ:267757 进行举报,一经查实,本站将立刻删除涉嫌侵权内容。
如果您发现有涉嫌版权的内容,欢迎发送邮件至:service@youtike.com 或 联系QQ:267757 进行举报,一经查实,本站将立刻删除涉嫌侵权内容。