甲、乙两车同时从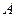 地出发,以各自的速度匀速向
地出发,以各自的速度匀速向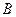 地行驶.甲车先到达
地行驶.甲车先到达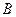 地,停留1小时后按原路以另一速度匀速返回,直到两车相遇.乙车的速度为每小时60千米.下图是两车之间的距离
地,停留1小时后按原路以另一速度匀速返回,直到两车相遇.乙车的速度为每小时60千米.下图是两车之间的距离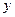 (千米)与乙车行驶时间
(千米)与乙车行驶时间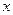 (小时)之间的
(小时)之间的 函数图象.
函数图象.
(1)两车行驶3小时后,两车相距 ▲ 千米;
(2)请在图中的( )内填上正确的值,并直接写出甲车从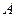 到
到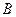 的行驶速度;
的行驶速度;
(3)求从甲车返回到与乙车相遇过程中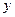 与
与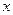 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量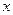 的取值
的取值
范围.
(4)求出甲车返回时的行驶速度及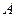 、
、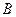 两地之间的距离.
两地之间的距离.
相关知识点
推荐套卷
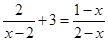 .
.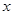 –1)+5<3
–1)+5<3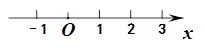

 粤公网安备 44130202000953号
粤公网安备 44130202000953号