如图,直线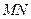 上方有平行于纸面且与MN成45°的有界匀强电场,电场强度大小为E;MN下方为方向垂直于纸面向里的有界匀强磁场,磁感应强度大小未知。今从MN上的O点向磁场中射入一个速度大小为v、方向与MN成45°角的带正电粒子,该粒子在磁场中运动时的轨道半径为R。若该粒子从O点进入磁场后第三次经过直线MN后又恰好通过O点。不计粒子的重力。求:
上方有平行于纸面且与MN成45°的有界匀强电场,电场强度大小为E;MN下方为方向垂直于纸面向里的有界匀强磁场,磁感应强度大小未知。今从MN上的O点向磁场中射入一个速度大小为v、方向与MN成45°角的带正电粒子,该粒子在磁场中运动时的轨道半径为R。若该粒子从O点进入磁场后第三次经过直线MN后又恰好通过O点。不计粒子的重力。求:
⑴粒子第三次经过直线MN时的位置;
⑵磁感应强度大小;
⑶粒子从O点出发到再次回到O点所需的时间。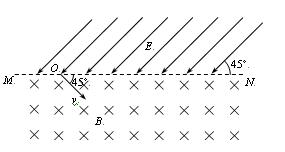
如图,直线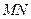 上方有平行于纸面且与MN成45°的有界匀强电场,电场强度大小为E;MN下方为方向垂直于纸面向里的有界匀强磁场,磁感应强度大小未知。今从MN上的O点向磁场中射入一个速度大小为v、方向与MN成45°角的带正电粒子,该粒子在磁场中运动时的轨道半径为R。若该粒子从O点进入磁场后第三次经过直线MN后又恰好通过O点。不计粒子的重力。求:
上方有平行于纸面且与MN成45°的有界匀强电场,电场强度大小为E;MN下方为方向垂直于纸面向里的有界匀强磁场,磁感应强度大小未知。今从MN上的O点向磁场中射入一个速度大小为v、方向与MN成45°角的带正电粒子,该粒子在磁场中运动时的轨道半径为R。若该粒子从O点进入磁场后第三次经过直线MN后又恰好通过O点。不计粒子的重力。求:
⑴粒子第三次经过直线MN时的位置;
⑵磁感应强度大小;
⑶粒子从O点出发到再次回到O点所需的时间。