如图所示,两根足够长固定平行金属导轨位于倾角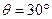 的斜面上,导轨上、下端各接有阻值
的斜面上,导轨上、下端各接有阻值 的电阻,导轨电阻忽略不计,导轨宽度
的电阻,导轨电阻忽略不计,导轨宽度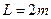 ,在整个导轨平面内都有垂直于导轨平面向上的匀强磁场,磁感应强度
,在整个导轨平面内都有垂直于导轨平面向上的匀强磁场,磁感应强度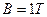 。质量
。质量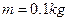 、连入电路的电阻
、连入电路的电阻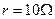 的金属棒
的金属棒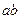 在较高处由静止释放,当金属棒
在较高处由静止释放,当金属棒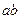 下滑高度
下滑高度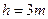 时,速度恰好达到最大值
时,速度恰好达到最大值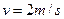 。金属棒
。金属棒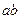 在下滑过程中始终与导轨垂直且与导轨良好接触。
在下滑过程中始终与导轨垂直且与导轨良好接触。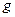 取
取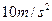 。求:
。求: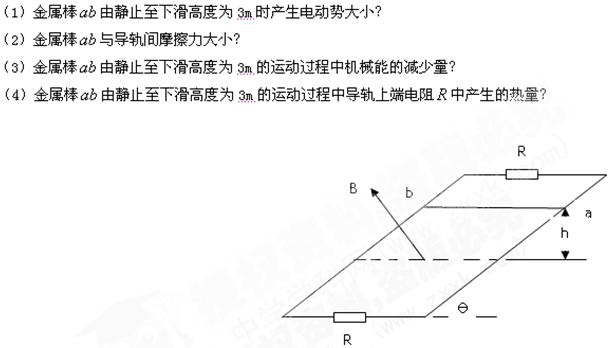
如图所示,两根足够长固定平行金属导轨位于倾角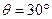 的斜面上,导轨上、下端各接有阻值
的斜面上,导轨上、下端各接有阻值 的电阻,导轨电阻忽略不计,导轨宽度
的电阻,导轨电阻忽略不计,导轨宽度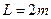 ,在整个导轨平面内都有垂直于导轨平面向上的匀强磁场,磁感应强度
,在整个导轨平面内都有垂直于导轨平面向上的匀强磁场,磁感应强度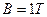 。质量
。质量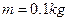 、连入电路的电阻
、连入电路的电阻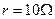 的金属棒
的金属棒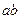 在较高处由静止释放,当金属棒
在较高处由静止释放,当金属棒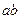 下滑高度
下滑高度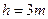 时,速度恰好达到最大值
时,速度恰好达到最大值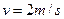 。金属棒
。金属棒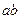 在下滑过程中始终与导轨垂直且与导轨良好接触。
在下滑过程中始终与导轨垂直且与导轨良好接触。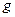 取
取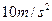 。求:
。求: