如图所示为某学校一套校内备用供电系统,由一台内阻为1Ω的发电机向全校22个教室( 每个教室有“220V,40W”的白炽灯6盏)供电。 白炽灯都正常发光。如果每条输电线的电阻R都是2Ω,升压变压器和降压变压器(都认为是理想变压器)的匝数比
每个教室有“220V,40W”的白炽灯6盏)供电。 白炽灯都正常发光。如果每条输电线的电阻R都是2Ω,升压变压器和降压变压器(都认为是理想变压器)的匝数比 分别是1:4和4:1,那么:
分别是1:4和4:1,那么: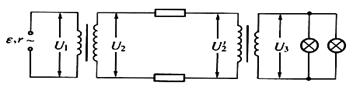
(1) 输电线上的电流是多大?
(2) 发电机的输出功率应是多大?
(3) 发电机的电动势是多大?
相关知识点
如图所示为某学校一套校内备用供电系统,由一台内阻为1Ω的发电机向全校22个教室( 每个教室有“220V,40W”的白炽灯6盏)供电。 白炽灯都正常发光。如果每条输电线的电阻R都是2Ω,升压变压器和降压变压器(都认为是理想变压器)的匝数比
每个教室有“220V,40W”的白炽灯6盏)供电。 白炽灯都正常发光。如果每条输电线的电阻R都是2Ω,升压变压器和降压变压器(都认为是理想变压器)的匝数比 分别是1:4和4:1,那么:
分别是1:4和4:1,那么:
(1) 输电线上的电流是多大?
(2) 发电机的输出功率应是多大?
(3) 发电机的电动势是多大?