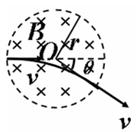如图所示,虚线所围区域内有方向垂直纸面向里的匀强磁场,磁感应强度为B。一束电子沿圆形区域的直径方向以速度v射入磁场,电子束经过磁场区后,其运动的方向与原入射方向成θ角。设电子质量为m,电荷量为e,不计电子之间的相互作用力及所受的重力。求:
(1)电子在磁场中运动轨迹的半径R;(2)电子在磁场中运动 的时间t;
的时间t;
(3)圆形磁场区域的半径r。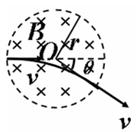
如图所示,虚线所围区域内有方向垂直纸面向里的匀强磁场,磁感应强度为B。一束电子沿圆形区域的直径方向以速度v射入磁场,电子束经过磁场区后,其运动的方向与原入射方向成θ角。设电子质量为m,电荷量为e,不计电子之间的相互作用力及所受的重力。求:
(1)电子在磁场中运动轨迹的半径R;(2)电子在磁场中运动 的时间t;
的时间t;
(3)圆形磁场区域的半径r。