汽车发动机的功率为60KW,汽车的质量为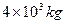 。当汽车在足够水平路面从静止以0.6m/s2的加速度做匀加速直线运动。求:
。当汽车在足够水平路面从静止以0.6m/s2的加速度做匀加速直线运动。求:
(1)汽车在水平路面能达到的最大速度vm1
(2)汽车在水平路面做匀加速运动能维持多长时间?
(3)在10s 末汽车的瞬时功率多大? 20s末汽车的瞬时功率又是多少呢?
(4)若汽车以vm1速度驶上一倾角为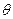 的足够长的斜面(
的足够长的斜面( )。简要描述汽车作何运动,并求出在此斜面上最终速度vm2(已知汽车在行驶中所受路面阻力恒定为重力的0.1倍,g取10m/s2)
)。简要描述汽车作何运动,并求出在此斜面上最终速度vm2(已知汽车在行驶中所受路面阻力恒定为重力的0.1倍,g取10m/s2)
汽车发动机的功率为60KW,汽车的质量为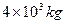 。当汽车在足够水平路面从静止以0.6m/s2的加速度做匀加速直线运动。求:
。当汽车在足够水平路面从静止以0.6m/s2的加速度做匀加速直线运动。求:
(1)汽车在水平路面能达到的最大速度vm1
(2)汽车在水平路面做匀加速运动能维持多长时间?
(3)在10s 末汽车的瞬时功率多大? 20s末汽车的瞬时功率又是多少呢?
(4)若汽车以vm1速度驶上一倾角为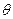 的足够长的斜面(
的足够长的斜面( )。简要描述汽车作何运动,并求出在此斜面上最终速度vm2(已知汽车在行驶中所受路面阻力恒定为重力的0.1倍,g取10m/s2)
)。简要描述汽车作何运动,并求出在此斜面上最终速度vm2(已知汽车在行驶中所受路面阻力恒定为重力的0.1倍,g取10m/s2)