用长L1=4m和长为L2=3m的两根细线，拴一质量m=2kg的小球A，L1和L2的另两端点分别系在一竖直杆的O1，O2处，已知O1O2=5m如下图（g＝10m·s-2）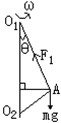
（1）当竖直杆以的角速度ω匀速转动时，O2A线刚好伸直且不受拉力．求此时角速度ω1．
（2）当O1A线所受力为100N时，求此时的角速度ω2．
相关试题
在图18－30中输电线总电阻为1Ω，输送的电功率P＝100kW．在下列两种情况下分别求出输电电流I，输电线上损耗的功率P损．①输电电压U输＝400V；②输电电压U输＝10kV．
如图1－8－18所示，水平放置的A、B两平行板相距h，有一质量为m，带电量为q的小球在B板之下H处以初速度v0竖直向上进入两板间，小球恰好能打到A板，求A、B板间的电势差.
图1－8－18
如图1－8－17所示，一平行板电容器接在U＝12 V的直流电源上，电容C＝3.0×10－10F，两极板间距离d＝1.20×10－3m，取g＝10 m/s2，求：
图1－8－17
(1)该电容器所带电量.
(2)若板间有一带电微粒，其质量为m＝2.0×10－3 kg，恰在板间处于静止状态，则该微粒带电量为多少？带何种电荷？
如图1－8－16所示，置于真空中的两块带电的金属板，相距1 cm，面积均为10 cm2，带电荷量分别为Q1＝2×10－8C，Q2＝－2×10－8C，若在两极板之间的中点放一个电荷量q＝5×10－9C的点电荷，求：金属板对点电荷的作用力是多大？
图1－8－16
粤公网安备 44130202000953号