在建筑工地上,我们常常看到工人用重锤将柱桩打入地下的情景。对此,我们可以建立这样一个力学模型:重锤的质量为m,从距桩顶高H处自由下落,柱桩的质量为M,重锤打击柱桩后不反弹且打击时间极短。柱桩受到地面的阻力恒为f,空气阻力忽略不计。利用这一模型,计算重锤一次打击柱桩时桩进入地下的深度h。
一位同学这样解:
设柱桩进入地面的深度为h,对全程运用动能定理,得: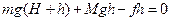
可解得:h=……
你认为该同学的解法是否正确?如果正确,请求出结果;如果不正确,请说明理由 ,并列式求出正确的结果。
,并列式求出正确的结果。
在建筑工地上,我们常常看到工人用重锤将柱桩打入地下的情景。对此,我们可以建立这样一个力学模型:重锤的质量为m,从距桩顶高H处自由下落,柱桩的质量为M,重锤打击柱桩后不反弹且打击时间极短。柱桩受到地面的阻力恒为f,空气阻力忽略不计。利用这一模型,计算重锤一次打击柱桩时桩进入地下的深度h。
一位同学这样解:
设柱桩进入地面的深度为h,对全程运用动能定理,得: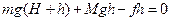
可解得:h=……
你认为该同学的解法是否正确?如果正确,请求出结果;如果不正确,请说明理由 ,并列式求出正确的结果。
,并列式求出正确的结果。