如图所示,光滑轨道上,小车A、B用轻弹簧连接,将弹簧压缩后用细绳系在A、B上.然后使A、B以速度v0沿轨道向右运动,运动中细绳突然断开,当弹簧第一次恢复到自然长度时,A的速度刚好为0,已知A、B的质量分别为mA、mB,且mA<mB. 求:
(1)被压缩的弹簧具有的弹性势能Ep.
(2)试定量分析、讨论在以后的运动过程中,小车B有无速度为0的时刻?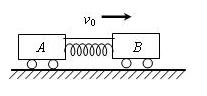
如图所示,光滑轨道上,小车A、B用轻弹簧连接,将弹簧压缩后用细绳系在A、B上.然后使A、B以速度v0沿轨道向右运动,运动中细绳突然断开,当弹簧第一次恢复到自然长度时,A的速度刚好为0,已知A、B的质量分别为mA、mB,且mA<mB. 求:
(1)被压缩的弹簧具有的弹性势能Ep.
(2)试定量分析、讨论在以后的运动过程中,小车B有无速度为0的时刻?