质量为M的小车左端放有质量为m的铁块且M>m，以共同速度v沿光滑水平面向竖直墙运动，车与墙碰撞的时间极短，不计动能损失。铁块与小车之间的动摩擦因数μ，车长为L，铁块不会到达车的右端，最终相对静止。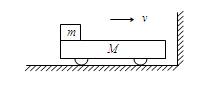
①求小车与铁块的最终速度；
②求整个过程中摩擦生热是多少？
相关试题
一不计重力的带电粒子质量为m，电量为+q，经一电压为U1平板电容器C1加速后，沿平行板电容器C2两板的中轴进入C2，恰好从C2下边缘射出。C2两板间电压为U2，长为L，如图所示。求平行板电容器C2上下两极板间距离d=？
已知O、A、B、C为同一直线上的四点、AB间的距离为l1,BC间的距离为l2,一物体自O点由静止出发，沿此直线做匀速运动，依次经过A、B、C三点，已知物体通过AB段与BC段所用的时间相等。求O与A的距离．
所示，两木快的质量分别为m1和m2，两轻质弹簧的劲度系数分别为k1和k2，上面木块压在上面的弹簧上（但不栓接），整个系统处于平衡状态，现缓慢向上提上面的木块，直到它刚离开上面弹簧，求在这过程中下面木块移动的距离。
．如图所示为甲乙两质点作直线运动的速度—时间图象，则下列说法中正确的是（）
| A．甲质点在0 ~ t1时间内的平均速度小于乙质点在0~t2时间内平均速度； | |
| B．甲质点在0 ~ t1时间内的加速度与
|
C．在0 ~ t3时间内甲、乙两质点的平均速度相等。 |
| D．在t3时刻，甲、乙两质点都回到了出发点。 |
粤公网安备 44130202000953号