长度为L=0.50m的轻质细杆OA，A端有一质量为m=3.0kg的小球，如图所示，小球以O点为圆心在竖直平面内做圆周运动。通过最高点时小球的速率是2.0m/s，g取10m/s2，则此时细杆OA受到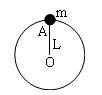 
| A．6N的拉力 |
| B．6N的压力 |
| C．24N的拉力 |
| D．24N的压力 |
相关试题
下列各项依次采用哪种方法最适宜
①鉴别一只羊是纯合子还是杂合子 ②在一对相对性状中区分显隐性
③不断提高小麦抗病品种的纯度 ④检验杂种遗传因子组成的方法
| A．杂交、自交、测交、测交 | B．测交、测交、杂交、自交 |
| C．测交、杂交、自交、测交 | D．杂交、杂交、杂交、测交 |
粤公网安备 44130202000953号