如图所示,质量m0="8" kg的小车放在光滑的水平面上,在小车右端加一水平恒力F=8N,当小车向右运动的速度达到1.5 m/s时,在小车前端轻轻放上一个大小不计、质量m="2" kg的小物块,物块与小车间的动摩擦因数μ=0.2,物块始终没有离开小车,g取10m/s2,求:
(1) 小物块在小车上滑动的时间。
(2) 从小物块被放上小车开始,经过t=2s小物块通过的位移大小。
(3) 要使物块始终没有离开小车,小车至少多长?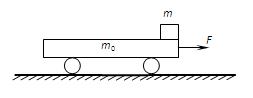
如图所示,质量m0="8" kg的小车放在光滑的水平面上,在小车右端加一水平恒力F=8N,当小车向右运动的速度达到1.5 m/s时,在小车前端轻轻放上一个大小不计、质量m="2" kg的小物块,物块与小车间的动摩擦因数μ=0.2,物块始终没有离开小车,g取10m/s2,求:
(1) 小物块在小车上滑动的时间。
(2) 从小物块被放上小车开始,经过t=2s小物块通过的位移大小。
(3) 要使物块始终没有离开小车,小车至少多长?