如图所示,斜面体固定在水平面上,斜面光滑,倾角为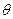 ,斜面底端固定有与斜面垂直的挡板,木板下端离地面高H,上端放着一个细物块。木板和物块的质量均为m,相互间最大静摩擦力等于滑动摩擦力
,斜面底端固定有与斜面垂直的挡板,木板下端离地面高H,上端放着一个细物块。木板和物块的质量均为m,相互间最大静摩擦力等于滑动摩擦力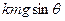 (k>1),断开轻绳,木板和物块沿斜面下滑。假设木板足够长,与挡板发生碰撞时,时间极短,无动能损失,空气阻力不计。求:
(k>1),断开轻绳,木板和物块沿斜面下滑。假设木板足够长,与挡板发生碰撞时,时间极短,无动能损失,空气阻力不计。求:
(1)木板第一次与挡板碰撞弹起上升过程中,物块的加速度;
(2)从断开轻绳到木板与挡板第二次碰撞的瞬间,木板运动的路程s;
(3)从断开轻绳到木板和物块都静止,摩擦力对木板及物块做的总功W.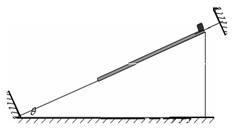
如图所示,斜面体固定在水平面上,斜面光滑,倾角为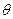 ,斜面底端固定有与斜面垂直的挡板,木板下端离地面高H,上端放着一个细物块。木板和物块的质量均为m,相互间最大静摩擦力等于滑动摩擦力
,斜面底端固定有与斜面垂直的挡板,木板下端离地面高H,上端放着一个细物块。木板和物块的质量均为m,相互间最大静摩擦力等于滑动摩擦力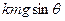 (k>1),断开轻绳,木板和物块沿斜面下滑。假设木板足够长,与挡板发生碰撞时,时间极短,无动能损失,空气阻力不计。求:
(k>1),断开轻绳,木板和物块沿斜面下滑。假设木板足够长,与挡板发生碰撞时,时间极短,无动能损失,空气阻力不计。求:
(1)木板第一次与挡板碰撞弹起上升过程中,物块的加速度;
(2)从断开轻绳到木板与挡板第二次碰撞的瞬间,木板运动的路程s;
(3)从断开轻绳到木板和物块都静止,摩擦力对木板及物块做的总功W.