用电阻为18Ω的均匀导线弯成如图所示直径D=0.80m的封闭金属圆环,环上AB弧所对圆心角为60,将圆环垂直于磁感线方向固定在磁感应强度B=0.50T的匀强磁场中,磁场方向垂直于纸面向里。一根每米电阻为1.25Ω的直导线PQ,沿圆环平面向左以 3.0m/s的速度匀速滑行(速度方向与PQ垂直),滑行中直导线与圆环紧密接触(忽略接触处的电阻),当它通过环上A、B位置时,求:
3.0m/s的速度匀速滑行(速度方向与PQ垂直),滑行中直导线与圆环紧密接触(忽略接触处的电阻),当它通过环上A、B位置时,求:
(1)直导线AB段产生的感应电动势,并指明该段直导线中电流的方向;
(2)此时圆环上发热损耗的电功率。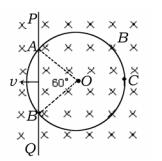
用电阻为18Ω的均匀导线弯成如图所示直径D=0.80m的封闭金属圆环,环上AB弧所对圆心角为60,将圆环垂直于磁感线方向固定在磁感应强度B=0.50T的匀强磁场中,磁场方向垂直于纸面向里。一根每米电阻为1.25Ω的直导线PQ,沿圆环平面向左以 3.0m/s的速度匀速滑行(速度方向与PQ垂直),滑行中直导线与圆环紧密接触(忽略接触处的电阻),当它通过环上A、B位置时,求:
3.0m/s的速度匀速滑行(速度方向与PQ垂直),滑行中直导线与圆环紧密接触(忽略接触处的电阻),当它通过环上A、B位置时,求:
(1)直导线AB段产生的感应电动势,并指明该段直导线中电流的方向;
(2)此时圆环上发热损耗的电功率。