如图所示,空间分布着方向平行于纸面且与场区边界垂直的有界匀强电场,电场强度为E、宽度为L。在紧靠电场右侧的圆形区域内,分布着垂直于纸面向外的匀强磁场,圆形磁场区域半径为r。当一带正电的粒子(质量为m,电荷量为q)从A点静止释放后,在M点离开电场,并沿半径方向射入磁场区域,磁感应强度为B,粒子恰好从N点射出,O为圆心,∠MON=120°,粒子重力忽略不计。求:
(1)粒子经电场加速后,进入磁场时速度v的大小;
(2)匀强磁场的磁感应强度B的大小和粒子在电场、磁场中运动的总时间t;
(3)若粒子在离开磁场前某时刻,磁感应强度方向不变,大小突然变为B1,此后粒子恰好被束缚在该磁场中,则B1的最小值为多少?
 转速和摆线的拉力?(取g=10m/s2)
转速和摆线的拉力?(取g=10m/s2)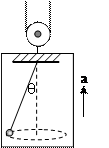

 飞出时,对轨道的压力恰好为零,则小球落地点C距A处多远?
飞出时,对轨道的压力恰好为零,则小球落地点C距A处多远?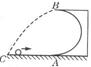


 粤公网安备 44130202000953号
粤公网安备 44130202000953号