如图,水平轨道AB与半径为R="1.0" m的竖直半圆形光滑轨道BC相切于B点.可视为质点的a、b两个小滑块质量ma=2mb="2" kg,原来静止于水平轨道A处,AB长为L=3.2m,两滑块在足够大的内力作用下突然分开,已知a、b两滑块分别沿AB轨道向左右运动,va = 4.5m/s,b滑块与水平面间动摩擦因数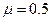 ,g取10m/s2.则
,g取10m/s2.则
(1)小滑块b经过圆形轨道的B点时对轨道的压力.
(2)通过计算说明小滑块b能否到达圆形轨道的最高点C.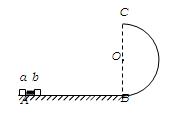
如图,水平轨道AB与半径为R="1.0" m的竖直半圆形光滑轨道BC相切于B点.可视为质点的a、b两个小滑块质量ma=2mb="2" kg,原来静止于水平轨道A处,AB长为L=3.2m,两滑块在足够大的内力作用下突然分开,已知a、b两滑块分别沿AB轨道向左右运动,va = 4.5m/s,b滑块与水平面间动摩擦因数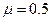 ,g取10m/s2.则
,g取10m/s2.则
(1)小滑块b经过圆形轨道的B点时对轨道的压力.
(2)通过计算说明小滑块b能否到达圆形轨道的最高点C.